why databases use b+ trees to hold data
so we all know most databases store data in b+ trees, but why? not just sql databases either - even non-relational databases like mongodb leverage b+ trees to store their data. mongodb's storage engine wiredtiger serializes collection data as b+ trees on disk. but let me tell you why there was even a need to introduce a data structure like b+ trees in the first place, and how this actually works in practice.
starting simple: the naive approach that doesn't work
let's start simple and see why the obvious approach fails spectacularly.
say our table records are stored in one file sequentially - literally one row after another in a single file. dead simple, right? when i say "row" here, i'm not just talking about sql tables. this applies to documents in mongodb, any entity you're storing - sql databases call them rows, nosql databases call them documents, but the idea holds true across the database spectrum.
the brutal reality of sequential storage
insert operations: o(n) complexity
here's the problem with inserting into a sequential file: you can easily append at the end, but what about inserting in the middle? databases typically store data ordered by primary key. so when you insert rows 1, 2, 5, then try to insert row 4...
you're screwed. why? you cannot just insert a line in the middle of a file. this isn't some in-memory buffer in your code editor where you hit enter and everything shifts down. on disk, when you write at a particular offset, you override what's there. period.
so what do you do? you have to:
- find the insertion position
- copy all rows before that position to a new file
- add the new row
- copy all remaining rows
- replace the old file
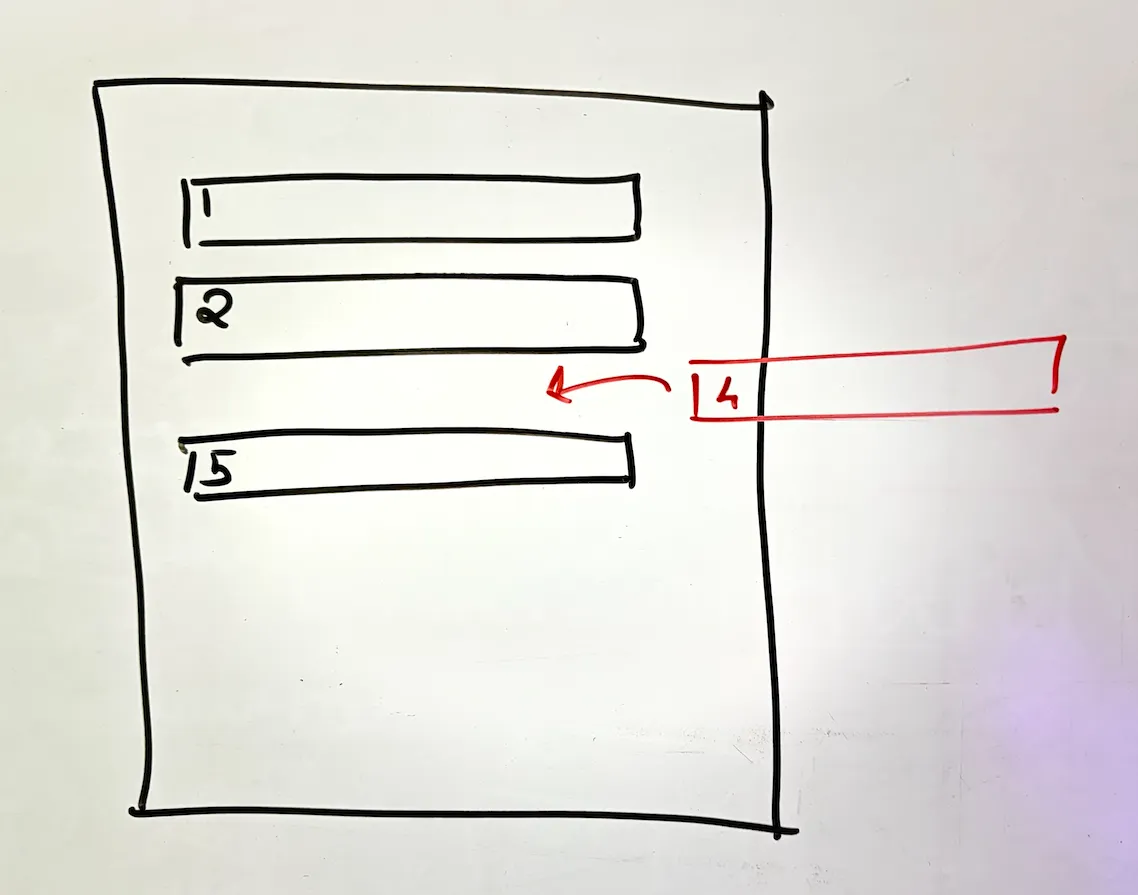
every. single. insert. creates a new file. that's o(n) complexity right there.
update operations: the width problem
updates are equally problematic. say you want to update row 3:
- linear scan to find it (worst case
o(n)) - start writing at that location
but wait - you can only write exactly the same number of bytes as the existing row. if the original row was 100 bytes and your update needs 120 bytes, those extra 20 bytes will override the beginning of row 4. you can't just push things forward - this is disk io, not ram.

so if you need more space? create a new file. copy everything. again.
find operations: pure linear scan
finding a single row? linear scan through the entire file. o(n). there's literally no other way with this structure.
range queries: slightly less terrible (but still bad)
range queries seem efficient once you find the first row - you can read sequentially from there. but finding that first row? still o(n).
delete operations: another new file
deleting row 3? you guessed it:
- find the row (
o(n)) - create new file
- copy everything except that row
- replace old file
the fundamental insight: o(n) complexity for every operation is far too much. we need something better.
enter b+ trees: the game changer
given that o(n) operations won't work for transactional databases, we need a better solution. this is where b+ trees come into the picture.
how b+ trees actually store your data
think about this: rows or documents in a table are clubbed together into b+ tree nodes.
let's get concrete with numbers:
- b+ tree node size: 4kb (matches disk block size)
- average row size: 40 bytes
- rows per node: 4kb ÷ 40 bytes ≈ 100 rows
why 4kb? this is crucial: disk io happens in blocks, typically 4kb. even if you want to read 1 byte, you read the entire 4kb block. the os does this for you - reads the block, extracts your byte, discards the rest. so we align our b+ tree node size with the disk block size. in one disk read, we read 1 node ≈ 100 rows.
the beautiful tree structure
your table becomes a collection of b+ tree nodes on disk. these nodes can be anywhere on the disk - they're not necessarily sequential. the database maintains the structure through pointers (disk offsets).
consider a table with 400 rows:
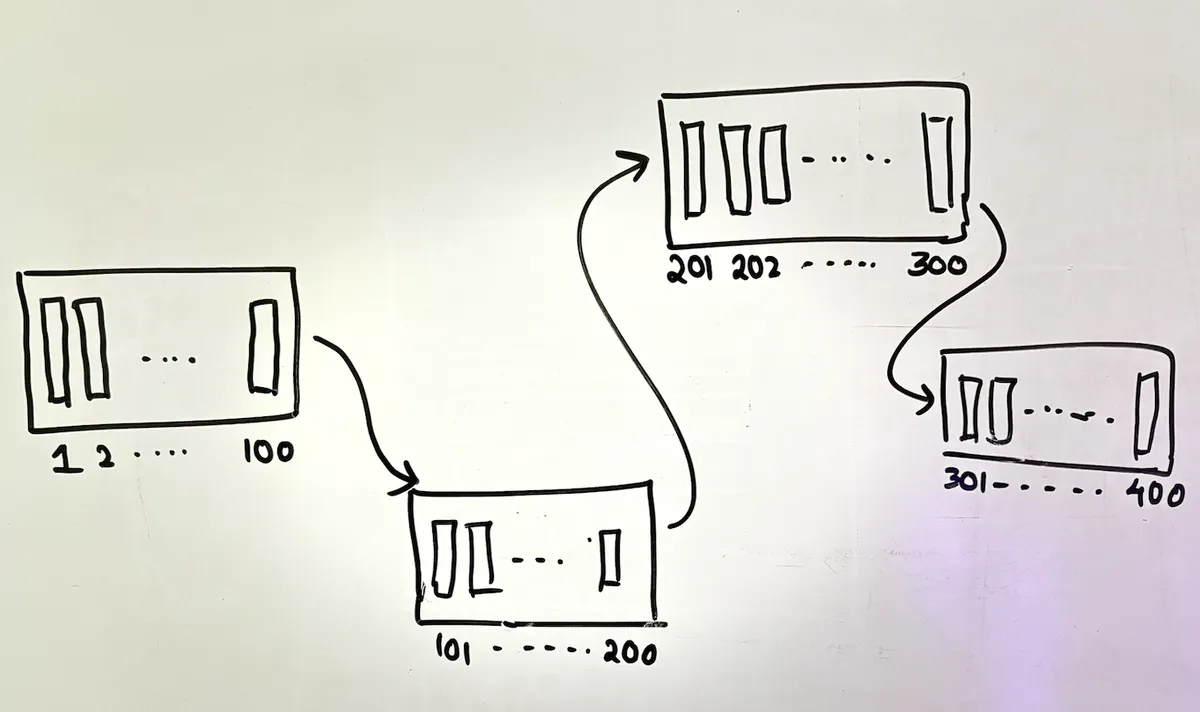
the table is always arranged by its primary key, and the b+ tree nodes (leaf nodes) are connected accordingly. but here's where it gets interesting...
the multi-level magic
a b+ tree isn't just leaf nodes. it has multiple levels:
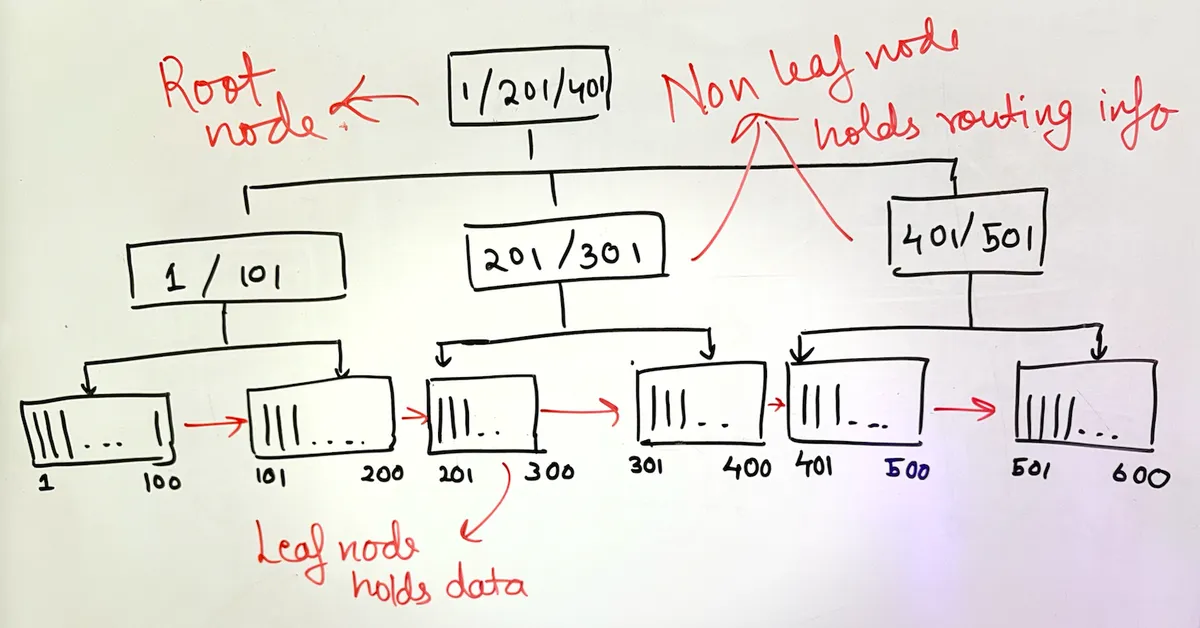
ps: sorry for my bad drawing :(
note: (leaf nodes linked linearly)
every b+ tree node is serialized and stored on disk. they're not in memory (though they can be cached there for performance).
non-leaf nodes hold routing information - they tell you which child node holds which range of data. the root might store [1, 201, 401], meaning:
- values < 201 are in the left subtree
- values 201-400 are in the middle
- values > 400 are in the right
leaf nodes hold the actual row data and are linked linearly to enable efficient range traversal.
operations in b+ trees: where the magic happens
find one by id: from o(n) to o(log n)
let's find row with id 3:
- read root node from disk - check routing info
- follow pointer to appropriate child - 3 is between 1 and 201
- read that node - 3 is between 1 and 101
- read leaf node - contains rows 1-100
- extract row 3 from the 100 rows in memory
total disk reads: 3 (for a 3-level tree). no matter which row you want, it's exactly 3 disk reads. not 1 extra.
insert: no more file rewriting
want to insert row 4?
- traverse to find the right leaf (3 disk reads)
- load that node into memory
- insert row 4 in the right position (array manipulation in ram)
- flush the node back to disk
that's it. we only touched the blocks we needed. no rewriting the entire file. the tree might need rebalancing (standard b+ tree stuff), but we're not touching unrelated nodes.
update: surgical precision
update row 202:
- navigate to the leaf (3 reads)
- load node into memory
- update the row
- flush back to disk
if the update changes the row size, we handle it in memory before flushing. no overwriting neighboring rows.
delete: clean and simple
delete row 401:
- find the leaf (3 reads)
- load into memory
- remove from array
- flush back
the tree might rebalance, but again, we're only touching what we need to. you can also do some kinda soft delete and do a batch delete later on by running a cron.
range queries: the secret weapon
this is where b+ trees truly shine. find all rows with id between 100 and 600:
- find the leaf containing 100 (3 reads)
- use the leaf-to-leaf links to traverse linearly
- read subsequent leaves until you reach 600
why b+ trees force you to store data at the leaf level: this linear traversal between leaves. b-trees allow data in non-leaf nodes, but b+ trees don't - precisely because it makes range queries super efficient. once you reach the first leaf, you just traverse sideways instead of going up and down the tree repeatedly.
the bottom line
this is why databases use b+ trees. the evolution from naive sequential storage to b+ trees solves fundamental problems:
- predictable performance:
o(log n)for single-row operations - efficient range queries: linear traversal at leaf level
- optimal disk io: node size matches disk block size
- localized updates: only touch the blocks you need
and this isn't just sql databases - mongodb's wiredtiger storage engine does exactly this. the beauty of b+ trees transcends the sql/nosql divide because the underlying problem - efficient disk-based storage with fast retrieval - is universal.
think about it: every operation that was o(n) in our naive approach is now o(log n) or better. that's the power of choosing the right data structure for your storage layer. and that's precisely why, when you dig into any production database, you'll find b+ trees at its heart.
key takeaways
- disk io constraints drive everything - you can't just insert in the middle of a file
- align data structures with hardware - b+ tree nodes match disk block size
- optimize for the common case - most database operations are finds and range queries
- trade complexity for performance - b+ tree maintenance is worth the
o(log n)guarantees
the next time someone asks why databases use b+ trees, you know it's not just tradition - it's physics, hardware constraints, and decades of engineering wisdom rolled into one elegant solution.